Introduction

Colloidal nanocrystals represent a class of structure-tunable functional materials, whose properties are intricately linked to their sizes and shapes1. Owing to their small dimensions and relatively large exposed surface area, nanocrystals exhibit versatile structural dynamics in specific chemical environments unlike their bulk counterparts2,3. Controlled manipulation allows the synthesis of diverse nanocrystals with precisely tuned structures4,5. Pre-synthesized nanocrystals are susceptible to subsequent structural restructuring in solution, including surface atom desorption and adsorption, coalescence, and dissolution followed by Ostwald ripening6,7. These nanocrystals further undergo chemical transformations under specific conditions, such as ion exchange, Kirkendall effect, and etching8,9,10,11.

Exploring spontaneous or chemically-driven structural changes in nanocrystals presents an efficient route to create nanocrystals with complex morphologies and properties unseen in conventional materials5,9. The scaling law and observed phenomena in these structural changes often deviate from expectations established at the bulk scale12. For instance, the solid-to-liquid transition (melting) of nanocrystals occurs at much lower temperatures than those of corresponding bulk materials13. This discrepancy can be attributed to the high ratio of surface-to-bulk atoms in nanocrystals, most of which are weakly bonded or under-coordinated and exert a substantial influence on structural transitions14,15. Additionally, as the size of a nanocrystal decreases, the influence of the surface atoms on the overall structure becomes more pronounced, which drives structural changes16. The ensemble of nanocrystals in solution inherently exhibits heterogeneity in their atomic structures for the same reason17.

To comprehensively understand the structural changes of nanocrystals, a method capable of directly imaging the 3D atomic structures of individual nanocrystals in solution is needed. The atomic spatial resolution of transmission electron microscopy (TEM) is the route to achieving this goal18,19. Atomic electron tomography (AET) is limited to capturing 3D atomic structures of nanocrystals exposed to vacuum and supported on a solid substrate20,21,22. Multiple AET scans of the same nanocrystal can be obtained for different time frames of a reaction by repeating the process of TEM imaging, pausing, and subjecting the nanocrystal to ex-situ reactions23. In cryogenic electron microscopy, 3D structures of particles, predominantly biological macromolecules, are obtained in frozen, hydrated states but represent the average of over tens of thousands of particles24. Liquid cell TEM25,26,27 allows for in-situ tracking of structural changes of individual nanocrystals in solution. Recent advancements demonstrated the ability to determine 3D atomic structures of individual solvated nanocrystals using high-resolution graphene liquid cell (GLC) TEM28,29.

In this work, we introduce ‘time-resolved Brownian tomography’ based on GLC TEM, enabling direct tracking of 3D atomic structural changes of single nanocrystals in solution over time. We apply this method to monitor the atomic structural changes of Pt nanocrystals undergoing oxidative etching in solution. The detachment and displacement of the atoms driving the etching process are captured. The 3D and time-resolved atomic-resolution tracking of nanocrystal etching reveals a transformation from an ordered face-centered cubic (FCC) to a highly disordered state when the nanocrystal reaches a diameter of ≈1 nm. This finding points to the emergence of a phase at the nanoscale, where surface complexity dominates the thermodynamic and kinetic properties.

Results and discussion

Time-resolved Brownian tomography of nanocrystals in liquid

We investigate the atomic-scale etching of Pt nanocrystals, employing time-resolved Brownian tomography. The etching of nanocrystals is ubiquitous in many chemical reactions of nanocrystals, from synthesis to corrosion, catalysis, and optoelectronics30,31,32. Tracking the etching of individual nanocrystals can also provide atomic-scale insights into size-dependent structures and thermodynamic properties of nanocrystals33,34. Since etching is generally understood as the specific desorption of surface atoms depending on the coordination environment of an atom and the chemical potential of the system35, high-index facets, kinks, and steps on nanocrystals are likely to facilitate the etching process36,37.

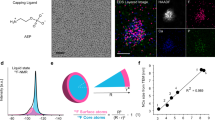
The time-resolved Brownian tomography is accomplished by deep-learning-assisted high-contrast millisecond GLC TEM and sequential application of the atomic-resolution 3D SINGLE29,38 methodology (Fig. 1). The Pt nanocrystals, passivated by polyvinylpyrrolidone (PVP) ligands, are contained in a GLC and images are captured with a temporal resolution of 2.5 ms using aberration-corrected TEM equipped with a direct electron detector (Methods). The presence of liquid can be confirmed by the generation of nanobubbles at lower imaging magnifications (Supplementary Fig. 1), the retarded translational motion of the nanocrystals (Supplementary Fig. 2 and Supplementary Note 1), and electron energy loss spectroscopy (EELS, Supplementary Figs. 3 and 4), as well as the etching39. The thickness of the liquid pocket from which high-resolution images of the nanocrystals are obtained is measured to be ≈10 nm (Methods, Supplementary Fig. 3, and Supplementary Note 2). In GLC TEM, oxidative etching of Pt nanocrystals is driven by radiolysis reactions taking place in a 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) buffer solution with Cl– anions, as supported by control experiments (Supplementary Note 3 and Supplementary Figs. 5 and 6)37,40,41. The PVP molecules on the Pt nanocrystals are likely to be degraded and detached by the radiolysis reactions prior to the etching, as indicated by the relaxation of tensile strain near the surface of a non-dissolving nanocrystal (Supplementary Note 4 and Supplementary Fig. 7)29. The noise in the raw TEM images is mitigated by a self-supervised denoising framework (Methods and Supplementary Figs. 8 and 9). The information-enhanced TEM image series maintains the original temporal resolution of 2.5 ms while clearly showing lattice patterns of the nanocrystals freely rotating in the GLC (Fig. 1a–d and Supplementary Movie 1), allowing for high-resolution 3D reconstruction with the reduced number of TEM images acquired for a few seconds.

Fig. 1: Time-resolved Brownian tomography of a Pt nanocrystal during etching.
figure 1

a Schematic illustration for Pt nanocrystals undergoing etching in a GLC. b Deep-learning-assisted high-contrast millisecond TEM for enhancing structural features of nanocrystals in millisecond-scale TEM images without compromising the temporal resolution. Raw images from a time-series GLC TEM are processed by the self-supervised denoising framework. The contrast of the raw image frames is adjusted (raw images without contrast adjustment are shown in Supplementary Fig. 9). c Selected denoised images from a time series. Denoised images are used for quantitative time-domain analysis. d Time-domain analysis on maximum FFT intensity of the denoised Pt nanocrystal images and the nanocrystal diameter obtained from the frames with high FFT intensity. Blue symbols denote frames with relatively high FFT intensity, and gray symbols denote frames with relatively low FFT intensity. The red line denotes moving-window average over 100 frames. e Reconstructed time-series 3D Coulombic density maps and atomic maps. Scale bars, 10 Å. Source data are provided as a Source Data file.

Full size image

The images with the high signal-to-noise ratio (SNR) obtained by the deep-learning-assisted high-contrast millisecond TEM are used for the quantitative time-domain analysis over the entire reaction trajectory (Methods). Based on the time-domain analysis, the extracted nanocrystal trajectory is divided into four sequential subsets: 0–5.1200 s (structure I), 7.5450–13.4550 s (structure II), 14.6975–17.2225 s (structure III), and 26.3100–34.2800 s (structure IV). The time period of each subset ensures sufficient sampling of image frames showing the rotating nanocrystal (Supplementary Fig. 10), while maximizing structural homogeneity of the nanocrystal in each subset. Over each subset, the size change of the nanocrystal occurs at sub-monolayer scale, smaller than 2.77 Å, the distance between Pt(111) planes (Fig. 1d). 3D structures obtained at a higher temporal resolution of 2–3 s indicate structural homogeneity during the early stage of etching (Supplementary Fig. 11).

Subsequently, the 3D reconstruction algorithm is applied to the predetermined subsets, resulting in four 3D Coulombic density maps—one from each time segment—from which the atomic positions are determined (Fig. 1b, Methods, Supplementary Fig. 12, and Supplementary Movie 2). The reconstruction method as well as the obtained 3D maps are validated (Supplementary Figs. 10, 13, and 14, and Supplementary Note 5). The average root-mean-square-deviations between the 3D structures reconstructed from the denoised images and the simulated image of the atomic maps are fewer than 0.31 Å (Supplementary Fig. 14c). The diameters, 1.97, 1.85, 1.83, and 1.36 nm, estimated from the time-series 3D atomic maps from the structures I to IV are consistent with the two-dimensional (2D) projected diameters measured from the periods over which the 3D maps are obtained (Supplementary Fig. 12c). As the nanocrystal shrinks by etching, its rotational motion becomes facilitated (Supplementary Fig. 15 and Supplementary Note 1).

Atomic structural dynamics of dissolving Pt nanocrystal

The atomic map analysis captures the etching process of the representative Pt nanocrystal (particle 1), as presented in Fig. 2, Supplementary Fig. 16, and Supplementary Movie 2. Initially (structure I), the Pt nanocrystal mostly follows a perfect FCC crystal structure, as represented by an A-B-C stacking sequence of (111) planes (Supplementary Fig. 12d). The 3D atomic map of structure I contains 314 atoms, which decrease to 264, 236, and 119 atoms in the following structures. No point defects and dislocations are observed within the 3D atomic maps. The 3D maps may have an uncertainty in their surface regions because we conservatively include atoms that are likely to exist throughout a reconstructed time period of 5 to 8 s (Methods). In this way, atoms that are adsorbed, desorbed, or largely diffused during each time period are excluded from the maps due to their resulting weak Coulombic densities in the 3D density maps which reflect the average structure. Nonetheless, since we applied an identical criterion for detecting atoms to the four structures, atomistic changes between each structure are captured consistently. The consistency between the atomic structures of the sub-divided maps and the original maps (Supplementary Fig. 11), as well as the stable time-series 3D structures of the non-dissolving nanocrystals (Supplementary Fig. 7), further indicates the reliability of the reconstruction method and the obtained atomic maps. The decreasing number of atoms at each time step indicates that the etch-rate is relatively slow (5–9 atoms s−1)42. This rate corresponds to sub-monolayer etching in a given size of the nanocrystal and the time interval of the observation.

Fig. 2: Time-series 3D atomic maps of a Pt nanocrystal during etching.
figure 2

a Time-series 3D atomic map of the Pt nanocrystals. Red spheres depict removed atoms, blue spheres depict rearranged atoms, and purple spheres depict atoms that are rearranged from the preceding maps and subsequently removed in the following maps. b–m Changes from structures I to II (b–e), II to III (f–i), and III to IV (j–m). b, f, j Locations of removed and rearranged atoms. d, e, h, i, l, m Atomic-scale changes in (100) and (1¯11) surfaces. c, g, k Local cross-correlations between two consecutive density maps shown for the (100) plane at the nanocrystal center. Atoms in the preceding and following maps are indicated with red and blue circles, respectively. The value of the local cross-correlation is indicated by the color scale. n–p Cross-correlation between structures I and II (n), structures II and III (o), and structures III and IV (p), presented along 〈100〉 (orange line), 〈110〉 (blue line), and 〈111〉 (green line) directions through the center of the 3D volume. Scale bars, 10 Å. Source data are provided as a Source Data file.

Full size image

We further investigate the dynamics of nanocrystal etching by tracking the positions of the same atoms over the time-series 3D maps aligned by rigid-body local optimization (Fig. 2, Supplementary Fig. 16, and Methods). Successful alignment of the structures is confirmed through cross-correlation analysis of consecutive density maps (Fig. 2n–p and Supplementary Fig. 16c), which are checked along all possible pairs of aligned crystal orientations with translational offsets. Then, comparing the position of each atom allows identification of identical atoms between two consecutive 3D maps and the subsequent determination of atoms lost from a preceding map and those that appear in the following map, as marked with red and blue spheres in Fig. 2a–m, respectively. The total number of atoms always decreases, so atoms appearing at a later time are attributed to atomic rearrangement; however, we cannot distinguish re-adsorption of dissolved Pt atoms and large surface diffusion of Pt atoms on the nanocrystal surface. Atom removal is predominant over atomic rearrangement in the entire etching process. The largest number of atoms are removed and rearranged between the structures III and IV where the nanocrystal is etched the most.

Etching of a surface is generally influenced by the extent to which surface atoms are stabilized by adjacent atoms43. The extent of atomic stabilization is related to atomic-scale factors such as coordination numbers, strain, and distances from neighboring atoms or bond length. The detailed views for selected Pt nanocrystal facets visualize the process of how individual atoms are sequentially detached from (100) and (1¯11) surfaces between structures I and II (Fig. 2d, e), II and III (Fig. 2h, i), and III and IV (Fig. 2l, m). Atoms are mainly removed from the kinks, steps, and small islands where they are under-coordinated (Supplementary Fig. 17). The 3D atomic maps also suggest that surface atoms with relatively higher coordination numbers, such as 8 and 9, are also removed in the later stage of the etching, between structures III and IV (Supplementary Fig. 17). This implies that the etching of smaller nanocrystals can be facilitated compared to larger ones and bulk surfaces. On the other hand, the radial strain and mean distance to the nearest Pt atoms (see below) do not show a clear distinction between removed and remaining surface atoms, suggesting that they have less impact on atomic stabilization compared to the coordination number in a given size range of the nanocrystal (Supplementary Fig. 18).

The atomic structural changes of the Pt nanocrystal become substantial as the etching proceeds. This is indicated by the cross-correlation graphs (Fig. 2n–p and Supplementary Fig. 16c), where the peak values decrease with time. We spatially analyze the structural changes by calculating the local cross-correlation of two consecutive 3D Coulombic density maps (Fig. 2c, g, k). The nanocrystal interiors mostly show correlation values close to unity, indicating that the inner structure of the nanocrystal is almost unchanged. The regions of low correlation are confined to the nanocrystal surface and are caused by the removal, rearrangement, and displacement of atoms. The structural changes in the nanocrystal become large near the surface regions between the structures III and IV.

The atomic displacements in the Pt nanocrystal induce deviations of individual atoms from an FCC structure. From structure I to II, almost every atom found in both structures shows little displacement (Fig. 3a), indicating that the overall structure of the nanocrystal remains similar except for the removed and rearranged atoms. The atomic displacements tend to increase from the nanocrystal center to the surface (Fig. 3b–d). The displacements of the interior atoms are comparable to the precision, 0.31 Å, estimated in our 3D atomic maps (Supplementary Fig. 14c), while the surface atoms are displaced up to 0.5 Å likely due to deficiencies in local coordination. As the etching continues, the surface atoms exhibit comparably larger displacements. The atoms showing large displacements are marked in Fig. 3a with arrows. The nanocrystal undergoes the most significant structural change between the structures III to IV, with some atoms displaced up to 2.5 Å. Such large atomic displacements lead to a substantial deviation of the nanocrystal surface structure from the FCC lattice, as shown in the (\(\overline{11}\)1) surface of the Pt nanocrystal (Fig. 3e, f). The atoms near the (\(\overline{11}\)1) surface generally follow the A-B-C stacking sequence of an FCC structure in structure III (Fig. 3e, f, cyan circles); however, the outermost atoms in structure IV are positioned directly above the atoms two layers beneath them showing an A-B-A stacking sequence of a HCP crystal (Fig. 3e, f, blue circles). The atoms associated with the small islands, kinks, and edges in the small-sized nanocrystal are unstable due to a deficiency in coordination, showing large atomic displacements (Fig. 3g and Supplementary Fig. 19a, b). Poorly-coordinated surface atoms can be stabilized by attractive interactions with adjacent atoms, as shown by reduced interatomic distances of surface atoms (Fig. 3h and Supplementary Fig. 19c, d) and contraction of surface atoms to the nanocrystal center (Fig. 3f). This is in accordance with a generally recognized phenomenon in which the lattice parameters of the metallic nanocrystals decrease as their sizes become smaller44,45,46.

Fig. 3: Atomic displacements during etching.
figure 3

a Displacements of atoms found in both structures I and II, structures II and III, and structures III and IV. Red spheres are atoms in the preceding map, and blue spheres are atoms in the following map. Semi-transparent spheres are defined to include the atoms in the preceding and following maps. The surfaces of those spheres are color-coded by atomic displacement and are indicated by the color scale. b–d Distributions of atomic displacements between atoms found in structures I and II (b), structures II and III (c), and structures III and IV (d). e, f Atomic structures of representative (¯1¯11) surfaces in structures III and IV, viewed from the directions normal (e) and parallel (f) to the (¯1¯11) surface. Cyan circles show the locations of surface atoms in the top layer of structure III. Blue circles show the locations of surface atoms in structure IV which are displaced relative to structure III. White circles show removed atoms. g Displacements of atoms between structures III and IV depending on coordination numbers obtained from structure III. h Mean Pt–Pt distances of individual surface Pt atoms in structures III (triangles) and IV (diamonds). Curves are Gaussian fits. Scale bars, 5 Å. Source data are provided as a Source Data file.

Full size image

Emerging structural disorder in dissolving Pt nanocrystal

The structural evolution of the Pt nanocrystal is further investigated by calculating the sixfold bond orientational order (BOO) parameter, Q6, as shown in Fig. 4a, Methods, Supplementary Fig. 20a, and Supplementary Movie 2. Initially (structure I), the nanocrystal structure is close to the FCC structure as almost all the atoms have Q6 of 0.57, expected for an ideal FCC crystal. As the etching proceeds, surface atoms located at the kink and step sites start to deviate from the FCC lattice as indicated by reduced Q6 (structure II). With further etching, more off-lattice atoms with smaller Q6 are identified (structure III). In the last structure, most of the surface atoms, as well as some of the inner atoms show strong deviation from the FCC lattice.

Fig. 4: Structural transformation during etching.
figure 4

a Time-series 3D atomic maps of the Pt nanocrystal, color-coded with the sixfold local BOO parameter, Q6. Scale bar, 10 Å. b Temporal evolution of the radial distribution function, g(r), of the time-series 3D atomic maps. Solid black lines indicate Gaussian fits to the first nearest-neighbor peaks. c Local BOO parameters obtained from time-series 3D atomic maps, depicted in (Q4, Q6) plane. (star) (Q4, Q6) = (0.19, 0.57) expected for a perfect FCC structure. (open triangle) (Q4, Q6) = (0.10, 0.48) expected for a perfect HCP structure. d Distributions of Q6 of the atoms in the four structures, presented over the distance from the nanocrystal center. e The atomic map of the structure IV, showing a crystalline core and disordered surface (Methods). f Ratio of the number of disordered atoms to the total number of atoms, Ndisordered/N, in the atomic maps. (circles) Particle 1. (triangles) Particle 2 (see Supplementary Note 6). (curve) Fit to the disordered atom fraction by an expression 1–A(d – dc)–n. Error bars indicate the time intervals over which the 3D atomic maps are obtained. g Ndisordered/N calculated from MD–MC simulations (Methods). The bold line and shaded region denote the average and standard deviation over ten MD–MC trajectories, respectively. Source data are provided as a Source Data file.

Full size image

The overall deviation of the nanocrystal structure from the FCC structure suggests that the nanocrystal experiences increased lattice strain as etching proceeds. A tensile strain of ≈1.3% is observed over the nanocrystal in the 3D radial strain map of structure I (Supplementary Fig. 21a, b), consistent with the reported 3D atomic structures of PVP-passivated Pt nanocrystals29,47. In structure II, regions with both reduced and stronger tensile strain are observed within the nanocrystal. The radial strain becomes stronger and more inhomogeneous in structures III and IV. The interatomic distances (Supplementary Fig. 21c), as well as the histograms of atomic radial strain (Supplementary Fig. 21d) also indicate that the strain distribution within the nanocrystal becomes inhomogeneous during etching.

The changes in the structural order of the Pt nanocrystal are quantitatively investigated by calculating structural parameters from the time-resolved 3D atomic coordinates. The radial distribution function, g(r), of structure I exhibits the pattern expected for an FCC lattice with relatively sharp peaks compared to ones from other structures (Fig. 4b). These peaks broaden and move to smaller distances over time, indicating decreasing nanocrystal crystallinity with slight lattice contraction by 0.15 Å from structures I to IV. Furthermore, the fourfold (Q4) and sixfold (Q6) BOO parameters of the atoms move to smaller values as the etching proceeds (Fig. 4c and Methods), further showing the reduced FCC-like symmetry in atomic arrangements. Noticeably, a significant portion of atoms in structure IV have BOO parameters similar to those of an HCP structure (Fig. 4c, open triangle), consistent with the observation in the 3D atomic map (Fig. 3e, f). We do not observe icosahedral order in any of the structures (Supplementary Fig. 20b). The degree of disorder, represented by smaller Q6, increases from the center to the surface of the nanocrystal (Fig. 4d).

For each map, the constituent atoms can be classified into two groups: crystalline atoms, where more than half of the bonds with its neighbors are crystalline bonds, and disordered atoms where half or less are crystalline bonds (see Methods and Supplementary Fig. 20c for details). In structure IV, crystalline atoms mostly exist at the core, while disordered atoms occupy a large volume near the surface, as shown in Fig. 4e. To examine how this disordered surface evolves, we calculate the fraction of disordered atoms, Ndisordered/N, which increases gradually as the nanocrystal shrinks (Fig. 4f). The Ndisordered/N is well described by the equation, 1–A(d–dc)–n, where d is the nanocrystal diameter and A, dc, and n are constants (Fig. 4f, red line). Similar expressions are often used to explain the thickness of a molten surface layer upon approaching a melting point48,49. Extrapolating the fit, the Pt nanocrystal is expected to be completely disordered at ≈1.3 nm. The disordering of the nanocrystal lattice, especially in structure IV, is observable in the denoised TEM images (Supplementary Fig. 22). Similar structural changes are observed for the time-series 3D structures of another Pt nanocrystal (particle 2, Supplementary Note 6, Supplementary Fig. 23).

Analysis of the denoised TEM images of additional Pt nanocrystals etched in a GLC confirms that the nanocrystal surface deviates from the FCC structure prior to the interior, followed by the disappearance of the FCC lattice around the diameters of 1.0–1.5 nm (Supplementary Fig. 24 and Supplementary Note 7). We also investigate the structures of the two types of Pt nanocrystals with varying sizes, synthesized either using PVP ligands or without using organic ligands in a flask, to check if nanocrystals experimentally synthesized with comparable sizes share the observed structural characteristics (Methods). The TEM images of the synthesized nanocrystals show the disappearance of the crystalline lattice as their size decreases to the sub-nanometer scale (Supplementary Fig. 25). Molecular dynamics and Monte Carlo (MD–MC) simulations also indicate that Pt nanocrystals exhibit disordered structures around 1 nm (Fig. 4g and Supplementary Fig. 26). This result provides a lower limit on the size of crystalline Pt nanoparticles in solution.

Previous studies claim that a disordered layer near the surface and its propagation to the interior can drive small nanocrystals to become completely disordered13,50,51. Other studies similarly claim that the contraction of metallic bonds at the surface destabilizes the ordered structures of nanocrystals45,46,52. However, a traditional and dominant idea may still be that small nanoclusters have highly symmetric (crystalline or icosahedral) structures34,53. Indeed, disordered clusters are generally accepted as a kinetically trapped state, as found in the descriptions of non-classical two-step nucleation models6,54. In this study, we experimentally show a spontaneous transition from a crystalline to a disordered state at a sufficiently low etch-rate whereby size-dependent thermodynamic stability is represented. The observation suggests that a disordered state could be considered as the stable state in metallic atom clusters45,46,52,55. It further implies that the thermodynamic origin of the well-known models for nucleation and crystallization needs articulation based on our observations of a new structure phase emerging at the cluster scale. These implications signify the value of our direct time-resolved 3D observation, which is an efficient way to track 3D atomistic changes of an individual nanocrystal in liquid.

In summary, we developed the time-resolved Brownian tomography method and applied it to identify the structural transformation of a Pt nanocrystal during etching in a solution. The time-resolved 3D atomic structures show that the disordered structures of small metal nanocrystals are consequences of stabilized poorly-coordinated atoms. This reveals how the structural stability of nanocrystals is related to their size. Our time-resolved Brownian tomography method has the potential to be utilized for investigating structural transitions of nanomaterials where atomic-scale structural fluctuations are important, such as growth, ion exchange, phase transitions, and defect generation and removal. With further development, our method can be applied to various materials, including metallic, semiconducting, and oxide nanocrystals, as well as soft matter and biological macromolecules, such as polymers, viruses, and proteins, in their native liquid phases. To achieve these goals, further development of liquid cells that reflect realistic reaction environments is needed. Additionally, to minimize unwanted changes in the specimens caused by the electron beam, advancements in low-dose, high-speed TEM techniques, and advanced image processing are necessary.

Methods

PVP-passivated Pt nanocrystal synthesis

Pt nanocrystals passivated with PVP ligands with diameters ranging from 2 to 3 nm were synthesized based on ref. 56. Briefly, 0.05 mmol of (NH4)2Pt(II)Cl4 (99.995%, Aldrich), 0.75 mmol of tetramethylammonium bromide (98%, Aldrich), 1 mmol of PVP (Mw 29 kg mol−1, Aldrich), and 10 mL of ethylene glycol (>99%, Aldrich) were mixed in a three-neck round bottom flask. Then, the mixture was heated to 160 °C and kept for 20 min. After cooling the solution to room temperature, 90 mL of acetone was added to precipitate the particles from the dispersion. The products were then centrifuged at 1000 × g for 5 min. The supernatant was discarded, and the Pt nanocrystals were collected. The nanocrystals were then redispersed in 5 mM HEPES buffer solution (>99.5%) with pH 7.4.

Unpassivated Pt nanocrystal synthesis

Unpassivated Pt nanocrystals with diameters ranging from 1 to 3 nm were synthesized based on ref. 57. Briefly, 0.193 mmol of H2Pt(II)Cl4·6H2O (>37.5% Pt, Aldrich), 2.5 mmol of sodium hydroxide (95%, Samchun), and 10 mL of ethylene glycol (>99%, Aldrich) were mixed in a three-neck round bottom flask. Then, the mixture was heated to 140 °C and kept for 3 h. After cooling the solution to room temperature, an excess of 1 M HCl (Aldrich) was added to precipitate the particles from the dispersion. The products were then centrifuged at 1000 × g for 5 min. The supernatant was discarded, and the Pt nanocrystals were collected. The nanocrystals were then redispersed in acetone.

GLC preparation

The procedure through which the GLCs were prepared is similar to ref. 29. Multilayer graphene was synthesized on a 25-μm-thick copper foil (99.8%, Alfa Aesar) by low-pressure chemical vapor deposition (CVD). The copper foil was inserted in a quartz tube and heated to 1000 °C for 30 min under a hydrogen flow of 10 cm3 min−1. The graphene was synthesized onto the copper foil under the flow of 25 cm3 min−1 methane and 10 cm3 min−1 hydrogen at 1000 °C. After 20 min, the furnace was rapidly cooled to room temperature with 25 cm3 min−1 methane flow. The intensity ratio of 2D to G bands ≈1 measured in Raman spectroscopy indicates that the graphene synthesized by this procedure has 3–5 layers (Supplementary Fig. 27). Using multilayer graphene allows for the observation of GLCs for up to 3 min while observing lattice structures of the Pt nanocrystals. Graphene-coated TEM grids were prepared by transferring the graphene to holey carbon TEM grids using a direct transfer method58. The graphene-covered copper foil was treated with weak oxygen plasma to remove graphene on one side of the foil. A gold TEM grid with perforated carbon film (Quantifoil) was placed onto the other side of the copper foil where graphene was not etched. Then, the copper foil substrate was etched with aqueous 0.1 g mL−1 ammonium persulfate (98.0%, Aldrich) solution. The graphene-coated TEM grid was washed with deionized water several times. The GLC was fabricated by sandwiching 0.5 μL of the Pt nanocrystal solution with two graphene-coated TEM grids. The as-prepared GLC was left in ambient condition for about 30 min before imaging to ensure the sealing of liquid. The optimization of both the GLC fabrication and the GLC TEM imaging conditions were checked using either a JEOL JEM-2100F microscope installed at the Center for Nanoparticle Research, Institute for Basic Science (IBS) or a JEOL JEM-ARM200F aberration-corrected microscope equipped with a Gatan K3 IS detector and installed at National Center for Inter-University Research Facility (NCIRF), South Korea.

Data acquisition

We imaged the GLCs in the regions where two holes of perforated carbon film overlay. In these regions, only the two sheets of graphene exist, providing higher resolution than other regions with supporting carbon film(s). The liquid pockets typically span over several hundred nanometers or up to a few micrometers with no defined shapes. The thickness of liquid pockets is typically less than 100 nm, as measured by EELS using the JEOL JEM-2100F microscope equipped with a Gatan GIF Quantum SE spectrometer. We imaged the edge of the GLCs where the liquid is as thin as 10 nm to get high-quality TEM datasets suitable for the 3D reconstruction (Supplementary Figs. 3, 28, 29 and Supplementary Note 2). The presence of the liquid in those regions was suggested from low-loss and core-loss EELS spectra, which shows the H2O exciton peak at ≈9 eV, and an N K edge at ≈402 eV and O K edge at ≈532 eV, respectively (Supplementary Figs. 3 and 4). The H2O exciton peak was not visible in a dry region without the liquid (Supplementary Fig. 3). We carefully chose a comparably weak electron beam current (61 pA) and short acquisition times (10−6 s for low-loss EELS, 0.5 s for core-loss EELS) to minimize unwanted electron beam-induced damages of fragile GLCs during EELS, although this imaging condition makes the spectra noisier than previous publications39,59,60. Furthermore, the presence of liquid in such thin regions under the similar electron dose rate and defocus used to obtain the main datasets for the Brownian tomography can also be confirmed by observing gas bubbles (Supplementary Fig. 30 and Supplementary Movie 3). The translational motion and the etching of Pt nanocrystals observed here further suggest the presence of liquid in this area, as these would not happen without the liquid39.

TEM movies of Pt nanocrystals in the GLCs were obtained with 400 frames s−1 using TEAM I, a modified FEI Titan 80–300 TEM equipped with a post-specimen geometric and chromatic aberration corrector and Gatan K2 IS direct electron detector. Thousands of images with 1920 × 1728 pixels and the pixel size of 0.358 Å were acquired at a dose rate of ≈15 e− Å−2 frame−1 at the acceleration voltage of 300 kV. The pixel size was confirmed based on the known lattice spacing of the graphene sheets containing the nanocrystals. The third-order spherical aberration coefficient of the image corrector is set to ~−11 μm. The images were acquired in “white-atom” contrast with a slight positive focus.

Ex-situ TEM images of Pt nanocrystals (Supplementary Fig. 25) synthesized with PVP ligands and without ligands were obtained with JEOL JEM-ARM200F TEM equipped with an image corrector, a cold field emission gun, and Gatan K3 IS Base direct electron detector. The images with a pixel size of 0.298 Å were acquired at a dose rate of ≈3000 e− Å−2 frame−1 and an acquisition time of 0.5 s at the acceleration voltage of 200 kV.

Model architectures for image denoising

We employed our network with dilated convolutions based on an efficient blind-spot network61. The architecture was designed to expect input map features with five dimensions, which includes the exact input frame and four nearby frames (Supplementary Fig. 8a). The exact input frame was processed with a 1 × 1 convolutional layer, whereas the nearby frames were treated with 3 × 3 convolutional layers (5 × 5 for 3 × 3 blind-spot) and 24 channels. Our model includes 14 layers of feature fusion blocks, each containing one 1 × 1 convolutional layer for feature fusion and five 3 × 3 convolutional layers for each frame. After each feature fusion block, the collected features were processed with 3 × 3 dilated convolutional layers for preserving the blind-spot constraint of the network and collected as the output feature.

Loss functions and blind-spot self-denoising framework

In training our blind-spot network, we implemented a mapping from time-series images x to denoised image x’. However, in the input of each prediction x, the center pixel (and nearby pixels in some cases) was excluded in the receptive field, \({{{\bf{x}}}}_{{{\rm{RF}}}(i)}\) of our network. For every single pixel i, we can define the blind-spot convolutional neural network (CNN) as the function,

$$f\left({{{{\bf{x}}}}_{{{\rm{RF}}}(i)}}; \theta \right)={{{\bf{x}}}^{{{\prime} }}}_{i}$$
(1)

where θ denotes the parameters of blind-spot CNN we want to train.

Unlike previous research, N2N and N2V showed that we can train denoising networks without clean ground truth62,63. In our training scheme, we train a blind-spot network by minimizing the same empirical risk as in N2V.

$${{{\rm{argmin}}}}_{\theta } {\sum } _{i} {\sum } _{j}L\left(f\left({{{{\bf{x}}}}_{{{\rm{RF}}}(i)}}^{j}; \theta \right)\right)={{{{\bf{x}}}^{{{\prime} }}}_{i}^{j}},{{{{\bf{x}}}}_{i}^{\, j}}$$
(2)

\({{{\bf{x}}}}_{i}^{j}\) is used as the target and the input for the network; the blind-spot network effectively erases the information of the original pixel, which prevents the network from learning the identity. For TEM observations, the statistics of noise are unknown for TEM images, and therefore, we use the L2 loss function to minimize the difference between the original and generated images.

$$L\left({{{\bf{x}}}}_{i}^{j},{{{\bf{x}}}^{{{\prime} }}}_{i}^{j}\right)={\left({{{\bf{x}}}}_{i}^{j}-{{{\bf{x}}}^{{{\prime} }}}_{i}^{j}\right)}^{2}$$
(3)

Training details

We used the noisy training dataset as a testing dataset without any pre-processing for evaluating the denoising framework. During training, we extract a randomly cropped image with 256 × 256 pixels in every frame to prevent the network from fully remembering noise patterns. Furthermore, we used data augmentation while training, and we randomly rotated each image by 90o and mirrored it vertically and horizontally.

We used a batch size of 16 for our blind-spot network training with a RAdam64 optimizer with a learning rate of 0.001. We used a warm-up and cosine annealing learning rate scheduler and 100 epochs for training. Our code is implemented with PyTorch and Lightning65,66, and training was performed with a single NVIDIA RTX 3090. We used the PyTorch native automatic mixed precision for training and inferencing to improve speed. We generated pre-processed patches cropped with 1024 × 1024 pixels with overlapping 256 pixels between patches for the initial dataset. A total of 10% of pre-processed patches are used for the training model. We use the batch size of 16 and the training took about 8 h and 6 h for inference denoised image.

The framework and training for denoising were validated using simulated TEM images of a model Pt nanocrystal in a GLC filled with liquid. The 3D atomic map in the structure IV of the main text was used as the Pt nanocrystal model. TEM simulation was performed with the detective quantum efficiency of a Gatan K2 detector and an electron dose of 10 e− Å−2 to match the experimental conditions. The other parameters used for the TEM simulation were identical to those used for the validation of the time-series 3D atomic maps (Supplementary Note 5). The results of the denoising process on the simulated TEM images are shown in Supplementary Fig. 8b. The denoised TEM images well recover the structural features of the model Pt nanocrystal, as compared with perfect TEM images, with a significant improvement of the mean peak SNR (PSNR) from 6.2 ± 0.4 to 19 ± 3 dB and the structural similarity index measure (SSIM) from 0.038 ± 0.002 to 0.27 ± 0.05 (Supplementary Fig. 8c). Applied to the experimental images, the structure of the Pt nanocrystal is observed more clearly (Supplementary Fig. 8d, e). To quantify the improvement of image quality, we estimated the SNR of the experimental datasets. The SNR of an object can be estimated from two independent measurements of the object67:

$${{\rm{SNR}}}=10\, {\log }_{10}\left(\frac{p}{1-p}\right)$$
(4)

where p denotes the cross-correlation coefficient between the two independent measurements. This relation was used to estimate the SNR of the original, 5 frames-averaged, and denoised nanocrystal trajectories by calculating p between two adjacent frames. The mean SNR increases from –7 ± 2 dB in the raw images to 14 ± 4 dB in the denoised images (Supplementary Fig. 8f). On the other hand, the mean SNR of the images moving-window-averaged by 5 frames is obtained to be 6 ± 4 dB. The lattice parameter of the Pt nanocrystals, calculated using Pt lattice peaks in the fast Fourier transforms (FFTs) of denoised TEM images, follows those from raw and 5-frame-averaged datasets with reduced fluctuation (Supplementary Fig. 8g), indicating more accurate measurement of the lattice parameter from the FFTs. Furthermore, the one-standard deviations in the Gaussian fits of the FFT peak of a representative frame from raw and denoised datasets are estimated to be ≈1.7 and ≈1.0 pixels, respectively. The difference can result in an ≈0.03 Å error in lattice parameter measurement. The increased SNR of the images would be favorable for time-resolved Brownian tomography, as it allows the use of fewer numbers of images to reconstruct a 3D structure at similar spatial resolution68,69.

It should be noted that the 3 × 3 blind spot used in the denoising framework reduces the information at the frequency near one-third of the sampling frequency, fs = 1/(pixel size), as seen in the FFT of a representative denoised TEM image (Supplementary Fig. 8e). Nonetheless, structural information of the nanocrystals mostly occurs at frequencies lower than fs/3 in our imaging condition, as seen in the image FFTs (Supplementary Fig. 8e). We also only used low-frequency information with the cutoff frequency of 2.3 Å in the 3D reconstruction process (please refer to the section “time-resolved Brownian tomography”) to prevent possible artifacts caused by the denoising framework.

2D image analysis

The times indicated in the time-series TEM images represent the time elapsed from the start of each observation, and the denoised TEM images were used for the analysis unless stated otherwise. Since the Pt nanocrystals exhibit rotational motion, the nanocrystals intermittently show clear lattice structures in the TEM images when the lattice is aligned with the observation direction and do not show these features when the lattice is misaligned. In addition, the translational motion of the nanocrystals along the out-of-plane direction of the GLC makes the nanocrystal move out of the narrow depth of focus, leading to the disappearance of the lattice for a few seconds. We identified the frames with visible nanocrystal lattices based on the maximum peak intensity in the FFTs of the extracted nanocrystal images55, which are obtained from the pre-processing step in the time-resolved Brownian tomography. The resulting plots, such as Fig. 1d, show a binary distribution of the maximum FFT peak intensities, which allow us to set a threshold value for discriminating the high-FFT-intensity-frames (aligned nanocrystal lattice) and low-FFT-intensity-frames (misaligned nanocrystal lattice).

The intense FFT peaks, detected when the nanocrystal lattice is aligned along the observation direction, can also be used to measure the nanocrystal size in the 2D images. We masked a pair of peaks in the FFT, and performed an inverse FFT operation using the masked peaks. A bilateral filter was applied to the inverse FFT, resulting in the image where the region with the nanocrystal lattice has higher pixel intensities. A binary image for the nanocrystal lattice was obtained by applying Otsu’s thresholding. This procedure is repeated for all the nanocrystal images with the high-FFT peak intensity. The projected diameter of the Pt nanocrystals shown in Fig. 1d was calculated using the area of the crystalline regions in the binarized image, by assuming a circular shape of the Pt nanocrystal projection in the TEM images. The projected diameter of the Pt nanocrystal shown in the main text (particle 1) decreases from ~2.4 to 1.8 nm over 34.2850 s.

Time-resolved Brownian tomography

The denoised TEM images were used for the following pre-processing steps and time-resolved 3D reconstruction. The center of mass of each Pt nanocrystal was tracked from the denoised TEM image after applying a low-pass filter with a 2.3 Å cutoff and a nonlinear filter to the images (Supplementary Fig. 2). TEM image sets for the time-resolved 3D reconstruction were then obtained by cropping the denoised images by an appropriate box size (160 pixels) around the center of mass of the nanocrystal. The time intervals from which time-resolved 3D structures are reconstructed are determined by considering three points: i) an accurate 3D structure is obtained using nanocrystal images observed from various directions29,38,70; ii) a more accurate 3D structure is reconstructed using images where the lattice plane of the nanocrystal is clearly visible38; iii) shorter time intervals are favored to increase the temporal resolution of the time-resolved reconstruction while ensuring the structural homogeneity during the intervals. Since the frames with strong nanocrystal lattice, identified as described in the last section, tend to appear during specific time intervals (Fig. 1d, blue symbols), we used these intervals for the time-resolved reconstruction. Although the periods without visible crystalline lattice are not used for the 3D structural determination, this approach allows for increasing the temporal resolution of our method. Simultaneously with detecting frames with strong nanocrystal lattice, the center of mass of the crystalline domain was detected by the inverse FFT operation and aligned with the center of the cropped image. 6192 high-crystallinity frames were obtained from 13,715 frames for particle 1, and 4604 high-crystallinity frames were obtained from 8566 frames for the particle 2. Based on the FFT intensity profile (Fig. 1d), the time periods for reconstructing particle 1 are determined to be: 0–5.1200 (structure I), 7.5450–13.4550 (structure II), 14.6975–17.2225 (structure III), and 26.3100–34.2800 s (structure IV). The time periods for the particle 2 are: 0–4.6150 (structure I), 5.2750–7.3275 (structure II), 9.1375–15.0875 (structure III), and 15.3000–21.4125 s (structure IV) (Supplementary Fig. 23). The resulting nanocrystal images were divided into subsets according to these determined time periods. The subsets for structure I to IV contain 1769, 1731, 819, and 1870 high-crystallinity frames for the particle 1, and 1254, 787, 1801, and 762 high-crystallinity frames for the particle 2.

3D Coulombic density maps of the Pt nanocrystals were reconstructed using the PRIME algorithm71, a core component of the 3D SINGLE methodology for 3D structural reconstruction from 2D TEM images. A spherical Pt nanocrystal with a perfect FCC crystal structure with sizes roughly similar to the mean 2D projected diameter over each time period was used as the initial model. The time-series 3D Coulombic density maps are obtained by independently applying the 3D reconstruction algorithm to each subset of denoised TEM images with a discrete search space of 2500 directions and a low-pass limit of 1.5 Å. Then, atomic positions were determined on the basis of the correlation between the experimental 3D Coulombic density map and a known atomic potential of Pt72. In this way, it is possible to distinguish Pt atoms from noises arise from the liquid background, and to accurately determine their positions. Some of the surface atoms with weak Coulombic densities, which probably detached and rearranged within a time interval of the reconstruction, also excluded by this method as well. The 3D atomic maps were then used as an initial model for the next iteration of 3D orientation refinement, and a total of five iterations of this 3D orientation refinement–atomic position determination were performed. The resulting 3D Coulombic density maps are presented as isosurfaces, and the atomic positions are presented as spheres in Fig. 1e and Supplementary Fig. 12. We observed that three blobs of distinctive Coulombic density located at the nanocrystal interior in the Structure III were not identified as atoms through our atomic position determination process, and thus they were excluded from the time-series structural analyses. The 3D Coulombic density maps and atomic position maps were visualized using UCSF ChimeraX73,74.

Time-series analysis

Quantitative analysis of the two consecutive 3D atomic maps in a time series requires perfect alignment of the atomic maps in 3D space. To do so, we performed rigid-body local optimization for two consecutive time-series 3D Coulombic density maps using USCF ChimeraX. The optimal alignment between the time-series 3D maps was confirmed by calculating cross-correlation (Fig. 2n–p and Supplementary Fig. 16c). We applied our atomic model building algorithm72 to the aligned 3D density maps to obtain 3D atomic maps, which were used for all the analysis. Identical atoms between the two aligned consecutive 3D atomic maps were then determined as the atoms closest to each other in the two maps. The result was verified manually, resulting in the identification of three types of atoms: those identified as the same in both maps, those only identified in the preceding map, and those only identified in the following map. For the first type of atoms, atomic displacements were calculated as shown in Fig. 3a–d. The calculated displacements are smaller than the nearest-neighbor distance of Pt, 2.77 Å. The second type of atoms originates from the removal of an atom from the nanocrystal in the preceding map, and they are referred to as removed atoms. The last type of atoms is presumably caused by the re-adsorption of Pt atoms suspended in the liquid to the nanocrystal surface, the large surface diffusion of atoms on the nanocrystal surface, or both. Those atoms are referred to as rearranged atoms.

Structure analysis

The coordinate of each atom in a 3D atomic map is used to characterize the structural evolution of the Pt nanocrystals. The BOO parameter defined by Steinhardt et al.75 is computed by the Python package Pyboo76. The local tensorial BOO parameter qlm of ith atom is calculated as

$${q}_{{lm}}\left(i\right)=\frac{1}{{N}_{i}}{\sum }_{j=1}^{{N}_{i}}{Y}_{{lm}}\left(\theta \left({{{\bf{r}}}}_{{ij}}\right),\phi \left({{{\bf{r}}}}_{{ij}}\right)\right)$$
(5)

where Ni is the number of bonds of the ith atom, Ylm is the spherical harmonics, rij is the vector connecting the ith and jth atoms, and l and m are integers with \(m \in [-l,+l ]\). The nearest neighbors of an atom are defined as atoms located within 3.41 Å, at which first minimum is observed in the g(r) plot, from the atom. The coarse-grained BOO parameter is calculated as

$${Q}_{{lm}}\left(i\right)=\frac{1}{{N}_{i}+1}\left({q}_{{lm}}\left(i\right)+{\sum }_{j=1}^{{N}_{i}}{q}_{{lm}}\left(j\right)\right),$$
(6)

which is further used to calculate rotationally-invariant coarse-grained BOO parameter as

$${Q}_{l}\left(i\right)=\sqrt{\frac{4{{\rm{\pi }}}}{2l+1}{\sum }_{m=-1}^{l}{\left|{Q}_{{lm}}\left(i\right)\right|}^{2}}$$
(7)

Ql(i) is used to color-code individual atoms in the 3D maps (Fig. 4a) and to investigate the local structures in the nanocrystal 3D maps. To classify disordered and crystalline atoms within the 3D maps, the dot product s6(i, j) of normalized complex vectors q6(i) and q6(j), was investigated77:

$${s}_{6}\left(i,j\right)={{{\bf{q}}}}_{6}\left(i\right)\cdot {{{\bf{q}}}}_{6}\left(j\right)={\sum }_{m=-6}^{6}{\widetilde{q}}_{6m}(i){\widetilde{q}}_{6m}{(j)}^{*}$$
(8)

where \({\widetilde{q}}_{6m}(i)\) is

$${\widetilde{q}}_{6m}\left(i\right)=\frac{{\bar{q}}_{6m}(i)}{{\left[{\sum }_{m=-6}^{6}{\left|{\bar{q}}_{6m}(i)\right|}^{2}\right]}^{1/2}}$$
(9)

If s6(i, j) is larger than a certain threshold value, the bond between ith and jth atoms can be considered crystalline78. We used the threshold value of 0.8, as every bond in a Pt nanocrystal with perfect FCC structure has s6 larger than 0.8. An atom with more than half of its bonds classified as crystalline is defined as a crystalline atom. Otherwise, an atom is classified as a non-crystalline atom. The distribution of s6 is provided in Supplementary Fig. 20c. Icosahedral structures (Supplementary Fig. 20b) can be identified by investigating wl, which is defined to be

$${w}_{l}={\sum}_{{m}_{1}+{m}_{2}+{m}_{3}=0}\left(\begin{array}{cc}l & l \qquad l\\ {m}_{1} & {m}_{2} \, \quad {m}_{3}\end{array}\right){q}_{l{m}_{1}}{q}_{l{m}_{2}}{q}_{l{m}_{3}}.$$
(10)

MD–MC simulation

To investigate the etching process of the Pt nanocrystals, we simulated the Pt atom dissolution processes by integrating MD–MC with the grand canonical ensemble79. We utilized a graph-CNN of the polarizable atom interaction neural network (PaiNN)80 for machine learning force field training with in-house generated first-principles dataset81. During the simulation, the chemical potential of Pt (μPt) was referenced to a bulk reservoir and set to 0.122 eV, of which conditions the Pt nanocrystal size of 1.0 nm dissolve82. For each simulation step, we first considered the insertion or dissolution of a Pt atom from the experimentally resolved Pt nanocrystal with the same probability.

$${{\rm{Insertion}}}:{{{\rm{Pt}}}}_{n}\to {{{\rm{Pt}}}}_{n}-1+{{{\rm{Pt}}}}^{2+}+\,\, {2{{\rm{e}}}}^{-}$$
(11)
$${{\rm{Dissolution}}}:{{{\rm{Pt}}}}_{n}-1+{{{\rm{Pt}}}}^{2+}+{2{{\rm{e}}}}^{-}\to {{{\rm{Pt}}}}_{n}$$
(12)

Then MC step was performed with the grand potential of the insertion and dissolution, as rewritten by

$$\Delta {G}_{{{\rm{insertion}}}}=E\left({{{\rm{Pt}}}}_{n}+1\right)-E\left({{{\rm{Pt}}}}_{n}\right)-E\left({{{\rm{Pt}}}}_{{{\rm{bulk}}}}\right)-{\mu }_{{{\rm{Pt}}}}$$
(13)
$$\Delta {G}_{{{\rm{dissolution}}}}=E\left({{{\rm{Pt}}}}_{n}-1\right)+E\left({{{\rm{Pt}}}}_{{{\rm{bulk}}}}\right)+{\mu }_{{{\rm{Pt}}}}-E({{{\rm{Pt}}}}_{n})$$
(14)

Here, E(Ptn) and E(Ptbulk) are the total energy of Pt nanocrystal of the previous step and Pt bulk, and E(Ptn+1) and E(Ptn−1) are the total energy of Pt nanocrystal after the insertion and dissolution process, respectively. MD simulation (200 fs simulated time at a constant temperature of 298 K) followed each MC step with a time step of 2 fs and the canonical ensemble using the Verlet algorithm83 as implemented in atomistic simulation environments84.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.